Abstractors and relational cross-attention: An inductive bias for explicit relational reasoning in Transformers

Awni Altabaa¹, Taylor Webb², Jonathan Cohen³, John Lafferty⁴
¹ Department of Statistics and Data Science, Yale University
² Department of Psychology, UCLA
³ Department of Psychology and Princeton Neuroscience Institute, Princeton University
⁴ Department of Statistics and Data Science, Wu Tsai Institute, Institute for Foundations of Data Science, Yale University

description Paper code Code experiment Experimental Logs

depiction of self-attention — Figure: A depiction of relational cross-attention (right), compared with standard self-attention (left). Relational cross-attention implements a type of information bottleneck to disentangle object-level features from relational features. When integrated into a broader Transformer-based architecture, this enables explicit relational representation, yielding improved abstraction and generalization from limited data.

Figure: A depiction of relational cross-attention (right), compared with standard self-attention (left). Relational cross-attention implements a type of information bottleneck to disentangle object-level features from relational features. When integrated into a broader Transformer-based architecture, this enables explicit relational representation, yielding improved abstraction and generalization from limited data.

Abstract

An extension of Transformers is proposed that enables explicit relational reasoning through a novel module called the Abstractor. At the core of the Abstractor is a variant of attention called relational cross-attention. The approach is motivated by an architectural inductive bias for relational learning that disentangles relational information from extraneous features about individual objects. This enables explicit relational reasoning, supporting abstraction and generalization from limited data. The Abstractor is first evaluated on simple discriminative relational tasks and compared to existing relational architectures. Next, the Abstractor is evaluated on purely relational sequence-to-sequence tasks, where dramatic improvements are seen in sample efficiency compared to standard Transformers. Finally, Abstractors are evaluated on a collection of tasks based on mathematical problem solving, where modest but consistent improvements in performance and sample efficiency are observed.

Method Overview

The ability to infer, represent, and process relations lies at the heart of human abilities for abstraction—by representing the relations between different situations, we are able to draw connections and synthesize new ideas. The Transformer architecture has the ability to model relations between objects implicitly through its attention mechanisms. However, we argue that standard attention produces entangled representations encoding a mixture of relational information and object-level features. In this work we propose an extension of Transformers that enables explicit relational reasoning through a novel module called the Abstractor and a new variant of attention called relational cross-attention.

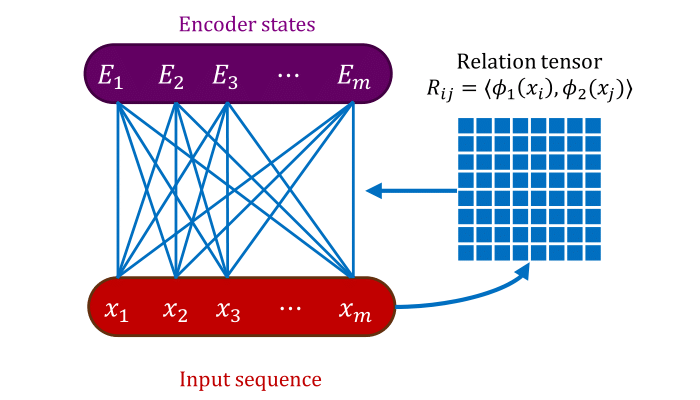
The core operation in a Transformer is attention. For an input sequence \(X = (x_1, \ldots, x_n)\), self-attention transforms the sequence via, \(X' \gets \phi_v(X) \, \mathrm{Softmax}({\phi_q(X)}^\top \phi_k(X))\), where \(\phi_q, \phi_k, \phi_v\) are functions on \(\mathcal{X}\) applied independently to each object in the sequence. We think of \(R := \phi_q(X)^\top \phi_k(X)\) as a relation matrix. Self-attention admits an interpretation as a form of neural message-passing as follows,

\[x_i' \gets \mathrm{MessagePassing}\left(\{(\phi_v(x_j), R_{ij})\}_{j \in [n]}\right) = \sum_{j} \bar{R}_{ij} \phi_v(x_j).\]

where \(m_{j \to i} = (\phi_v(x_j), R_{ij})\) is the message from object \(j\) to object \(i\), encoding the sender’s features and the relation between the two objects, and \(\bar{R} = \mathrm{Softmax}(R)\) is the softmax-normalized relation matrix. Hence, the processed representation obtained by self-attention is an entangled mixture of relational information and object-level features.

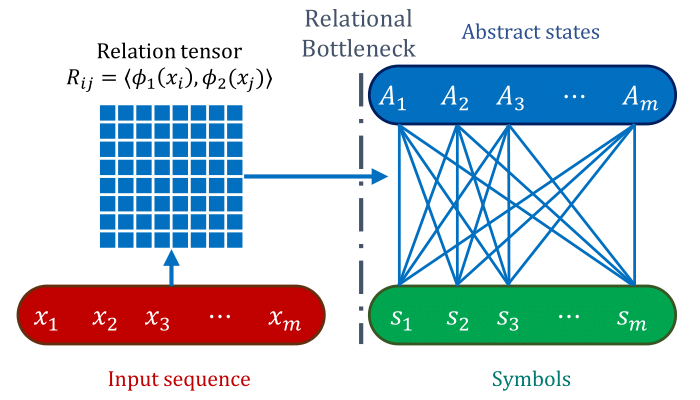
Our goal is to learn relational representations which are abstracted away from object-level features in order to achieve more sample-efficient learning and improved generalization in relational reasoning. This is not naturally supported by the entangled representations produced by standard self-attention. We achieve this via a simple modification of attention—we replace the values \(\phi_v(x_i)\) with vectors that identify objects, but do not encode any information about their features. We call those vectors symbols. Hence, the message sent from object \(j\) to object \(i\) is now \(m_{j \to i} = (s_j, R_{ij})\), the relation between the two objects, together with with the symbol identifying the sender object,

\[A_i \gets \mathrm{MessagePassing}\left(\{(s_j, R_{ij})\}_{j \in [n]}\right)\]

Symbols act as abstract references to objects. They do not contain any information about the contents or features of the objects, but rather refer to objects.

Abstraction relies on the assignment of symbols to individual objects without directly encoding their features. We propose three different mechanisms for assigning symbols to objects: positional symbols (symbols are assigned to objects sequentially based on the order they appear), position-relative symbols (symbols are assigned to encode the relative position of the sender with respect ot the receiver), and symbolic attention (symbols are retrieved via attention from a library of learned symbols).

This motivates a variant of attention which we call relational cross-attention. Relational cross-attention forms the core of the Abstractor module. The Abstractor processes a sequence of objects to produce a sequence of “abstract embeddings” which encode the relational features among its input.

Please see the paper for the details.

Experiments

We evaluate our proposed architecture on a series of experiments involving both discriminative and generative tasks. We compare to a standard Transformer as well as to previous relational architectures. Please see the paper for a description of the tasks and the experimental set up. We include a preview of the results here.

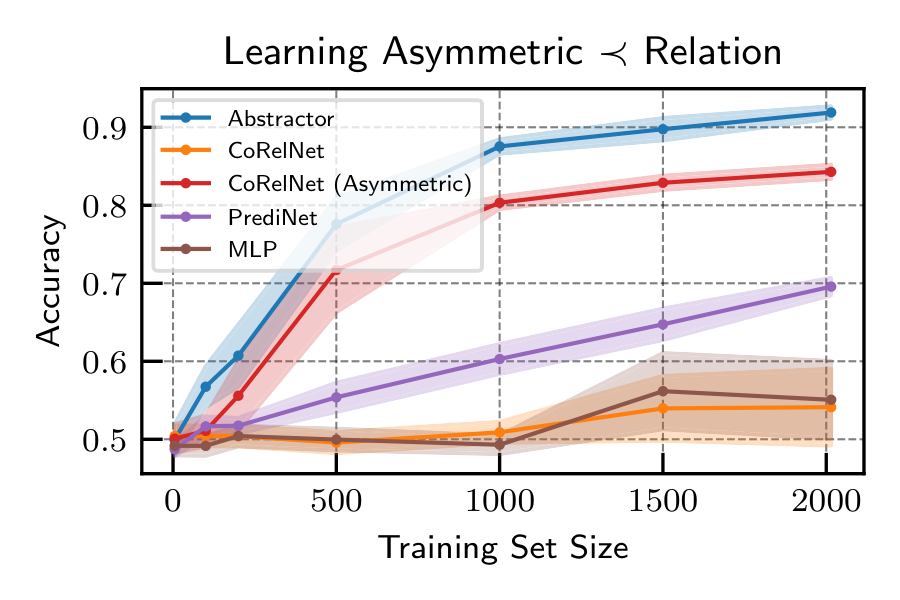
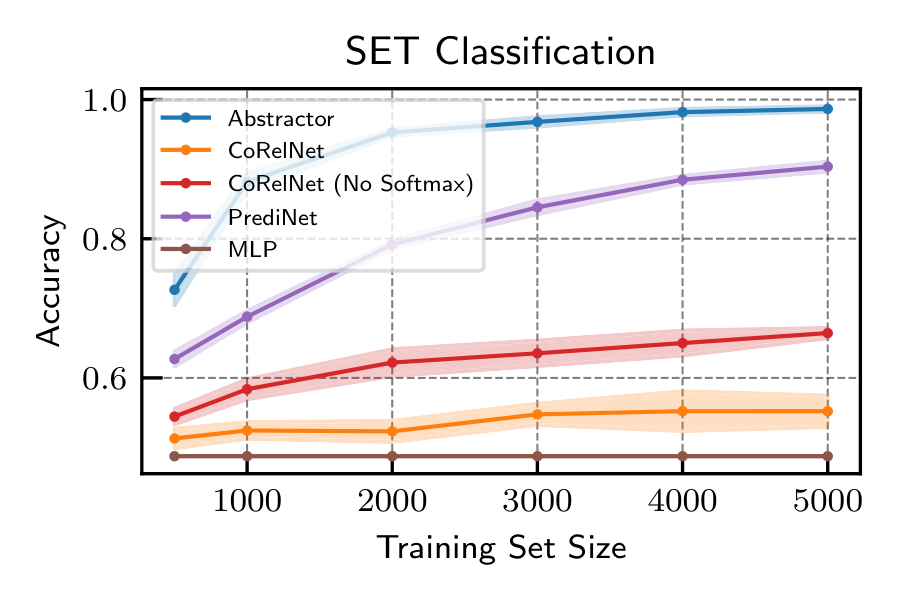
Discriminative Relational Tasks. We begin our experimental evaluation with discriminative relational classification tasks—a setting where it is possible to compare to previously proposed relational architectures such as PrediNet and CoRelNet. THe figure below compares sample-efficiency at two discriminative relational tasks: modeling transitive pairwise order in random objects and a task based on the SET card game. We find that explicitly relational architectures always outperform an MLP, with the Abstractor being the best-performing model on these tasks.

learning curves of pairwise order discriminative task — Figure: Learning curves on the discriminative relational tasks. Modeling transitive pairwise order in random objects (left) and a task based on the SET game (right).

learning curves on SET game classification task — Figure: Learning curves on the discriminative relational tasks. Modeling transitive pairwise order in random objects (left) and a task based on the SET game (right).

Random Object Sorting. Next, we evaluate a sequence-to-sequence relational task and compare to a standard Transformer. The task is to autoregressively predict the argsort of a sequence of randomly-generated objects. The underlying order relation must be learned from data in an end-to-end fashion. We observe the Abstractor-based model to be dramatically more sample-efficient at this task. Moreover, the Abstractor is able to generalize to new but similar tasks.

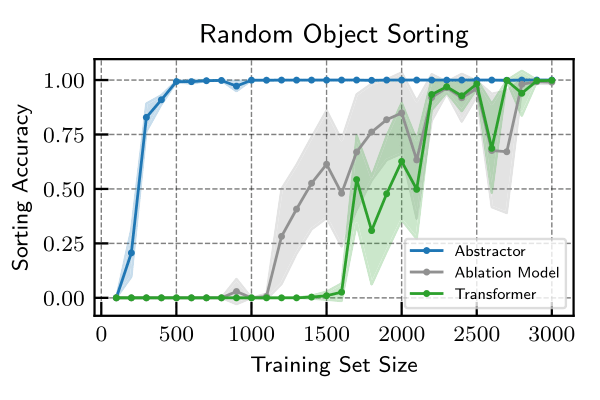
learning curves for object-sorting experiments — Figure: Learning curves on autoregressive object-sorting task (left) and learning curves after pre-training on a similar but different object-sorting task (right).

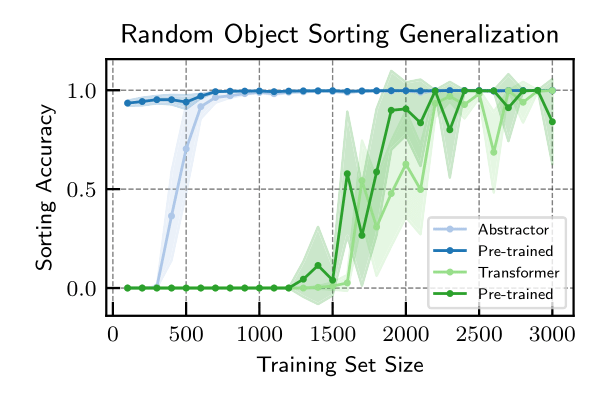
learning curves for object-sorting experiments after pre-training on related task — Figure: Learning curves on autoregressive object-sorting task (left) and learning curves after pre-training on a similar but different object-sorting task (right).

Mathematical Problem-Solving. Finally, we evaluate the Abstractor on a sequence-to-sequence task which is more representative of the complexity of real-world tasks: solving mathematical problems. The mathematical problems includes the following tasks: differentiation (calculus), predicting the next term in a sequence (algebra), solving linear equations (algebra), expanding products of polynomials, and adding polynomials. We observe a consistent and notable improvement in performance and sample efficiency.

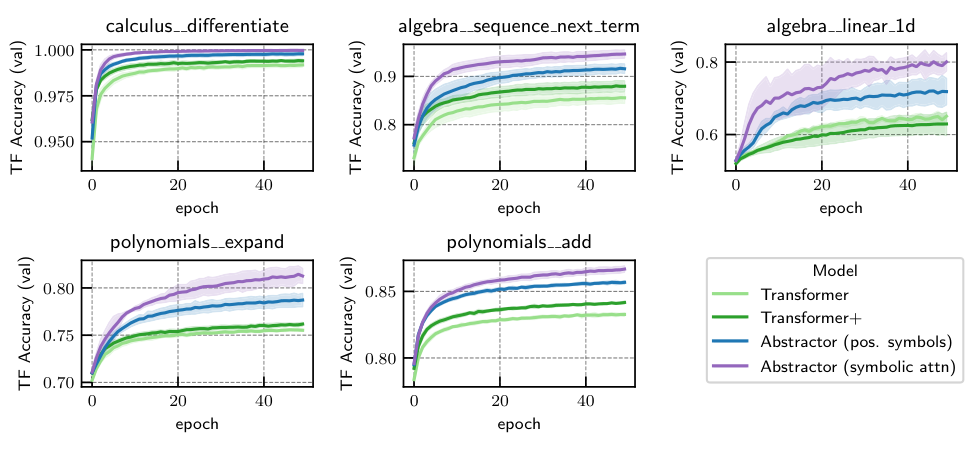
Learning Curves of Mathematical Problem-Solving Tasks — Figure: Training curves on mathematical problem-solving tasks.

Please see the paper for details on these experiments.

Experiment Logs

Detailed experimental logs are publicly available to help promote reproducibility and transparency. They include training and validation metrics tracked during training, test metrics after training, code/git state, resource utilization, etc. Experimental logs for all experiments in the paper can be accessed through the following web portal.

Citation

@article{altabaa2023abstractors,
      title={Abstractors and relational cross-attention: An inductive bias for explicit relational reasoning in Transformers}, 
      author={Awni Altabaa and Taylor Webb and Jonathan Cohen and John Lafferty},
      year={2023},
      eprint={2304.00195},
      archivePrefix={arXiv},
      primaryClass={stat.ML}
}