Relational Convolutional Networks: A framework for learning representations of hierarchical relations

Abstract

A maturing area of research in deep learning is the study of architectures and inductive biases for learning representations of relational features. In this paper, we focus on the problem of learning representations of hierarchical relations, proposing an architectural framework we call ``relational convolutional networks’’. Given a collection of objects, pairwise relations are modeled via inner products of feature maps. We formalize a relational convolution operation in which graphlet filters are matched against patches of the input (i.e, groupings of objects), capturing the relational pattern in each group of objects. We also propose mechanisms for explicitly learning groupings of objects which are relevant to the downstream task. Composing these operations yields representations of higher-order, hierarchical relations. We present the motivation and details of the architecture, together with a set of experiments to demonstrate how relational convolutional networks can provide an effective framework for modeling relational tasks that have hierarchical structure.

Method Overview

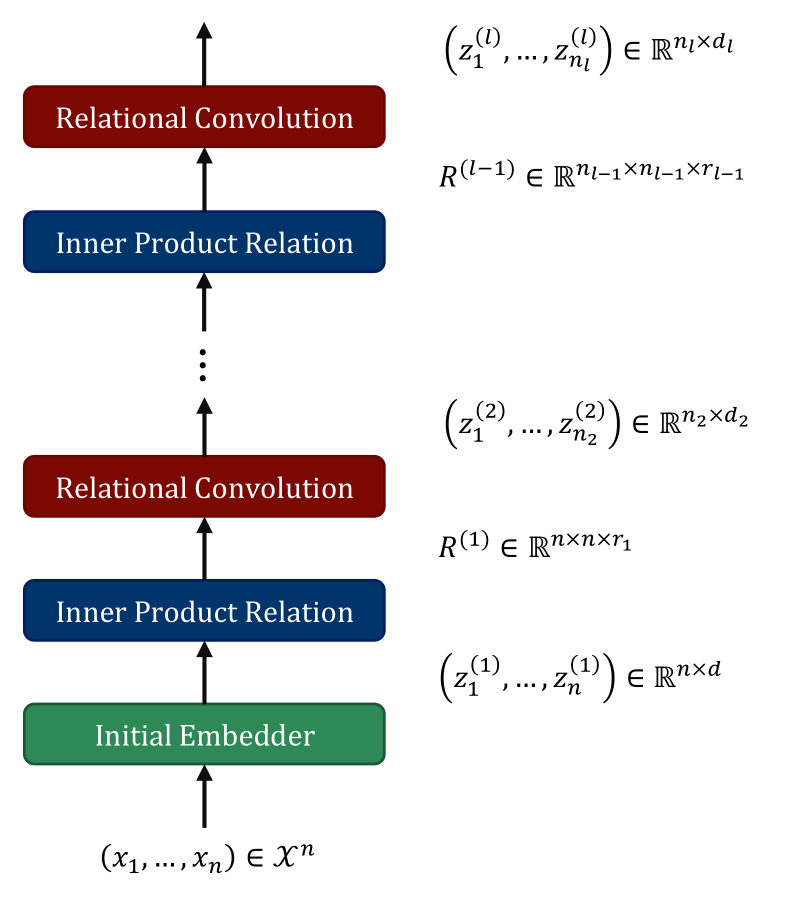
Compositionality—the ability to compose modules together to build iteratively more complex feature maps—is key to the success of deep representation learning. For example, in a feed forward network, each layer builds on the one before, and in a CNN, each convolution builds an iteratively more complex feature map. So far, work on relational representation learning has been limited to “flat” first-order architectures. In this work, we propose a compositional framework for learning hierarchical relational representations, which we call “relational convolutional networks.”

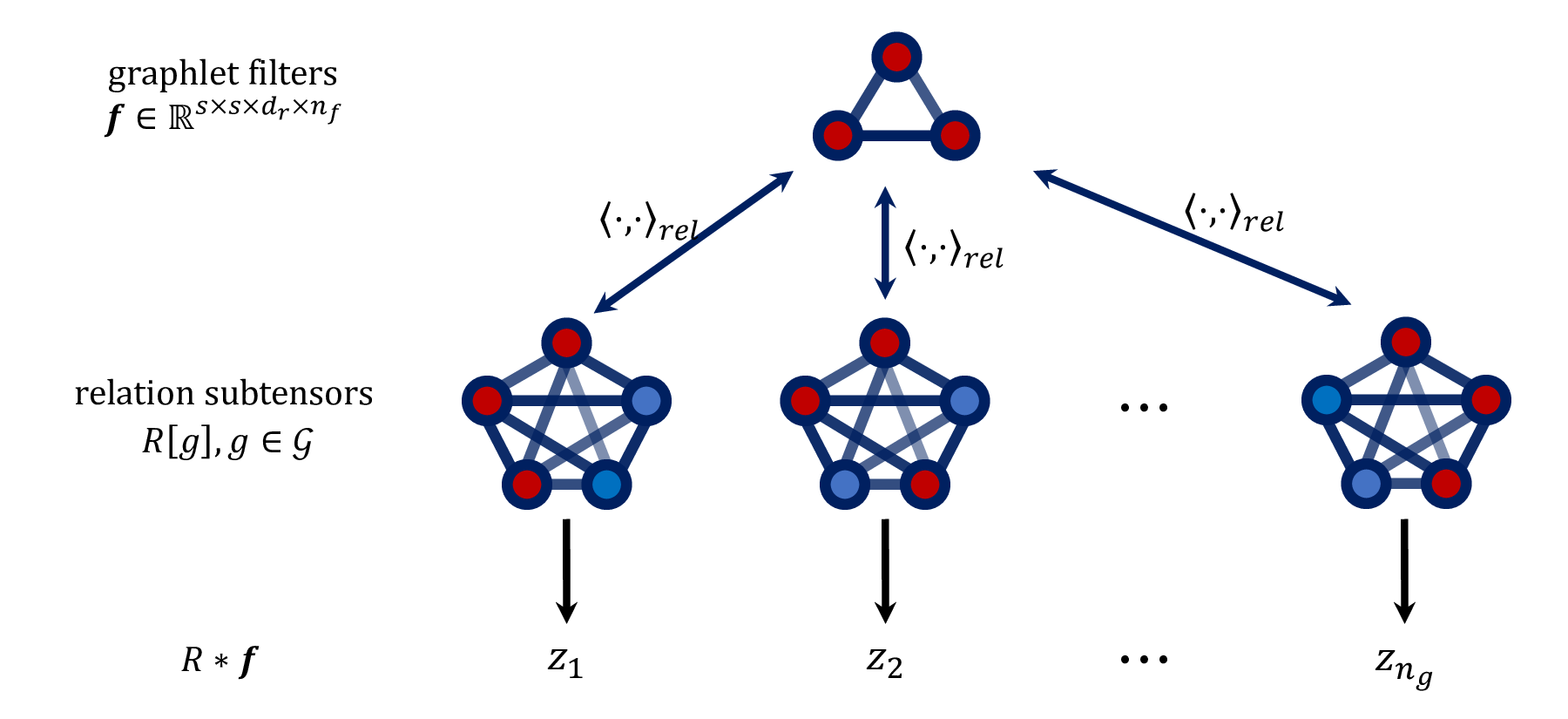
A schematic of the proposed architecture is shown in the figure to the right. The key idea involves formalizing a notion of “convolving” a relation tensor, describing the pairwise relations in a sequence of objects, with a “graphlet filter” which represents a template of relations between subsets of objects. Each composition of those operations computes relational features of a higher order.

Multi-Dimensional Inner Product Relation Module. The “Multi-dimensional Inner Product Relation” (MD-IPR) module receives a sequence of objects \(x_1, \ldots, x_m\) as input and models the pairwise relations between them, returning an \(m \times m \times d_r\) relation tensor, \(R[i,j] = r(x_i, x_j)\), describing the relations between each pair of objects.

Relational Convolutions. The relational convolution operation does two things: 1) extracts features of the relations between groups of objects using pairwise relations 2) transforms the relation tensor back into a sequence of objects, allowing it be composed with another relational layer to compute higher-order relations. In a relational convolution module, we learn a set of “graphlet filters,” which form a template of relations among a subset of the objects (a graphlet). The output of a relational convolution operation is a sequence of objects \(R \ast \boldsymbol{f} = \left(\langle R[g], \boldsymbol{f} \rangle_{\mathrm{rel}} \right)_{g \in \mathcal{G}} = (z_1, \ldots, z_{n_g})\) where each output object represents the relational pattern within some group of input objects, obtained through an appropriately-defined inner-product comparison with the graphlet filters.

Grouping layers. Rather than considering the relational patterns within all groups of objects, we explicitly model and determine relevant groupings through an attention operation.

Please see the paper for more details on the proposed architecture.

Experiments

We evaluate our proposed architecture on two sets of relational tasks: relational games and SET. We compare against previously proposed relational architectures, PrediNet and CoRelNet. We also compare against Transformers. Please see the paper for a description of the tasks and the experimental set up. We include a preview of the results here.

Relational games. The relational games benchmark allows us to evaluate out-of-distribution generalization. The dataset consists of a series of classification tasks involving a set of objects. In the figure below, we show generalization performance on two sets of objects different from those used during training.

SET. SET is a card game which forms a simple but challenging relational task. To solve the task, one must process the sensory information of individual cards to identify the values of each attribute, then somehow search over combinations of cards and reason about the relations between them. This is a task which tests a model’s ability to represent and reason over relations among subgroups of objects. This is a capability built explicitly into relational convolutional networks, but is missing from other relational models.

Finally, we explore the geometry of the learned representations in relational convolutional networks. As a preview, the figure below depicts the geometry of the relational convolution operation, demonstrating its ability to learn compositional features.

Experiment Logs

Detailed experimental logs are publicly available. They include training and validation metrics tracked during training, test metrics after training, code/git state, resource utilization, etc.

Relational games. For code and instructions to reproduce the experiments, see this readme in the github repo. The experimental logs for each task can be found at the following links: same, occurs, xoccurs, between, and match pattern.

SET. For code and instructions to reproduce the experiments, see this readme in the github repo. The experimental logs can be found here.

Citation

@article{altabaa2023relational,
      title={Relational Convolutional Networks: A framework for learning representations of hierarchical relations}, 
      author={Awni Altabaa and John Lafferty},
      year={2023},
      eprint={2310.03240},
      archivePrefix={arXiv},
      primaryClass={cs.LG}
}