Disentangling and Integrating Relational and Sensory Information in Transformer Architectures

Awni Altabaa, John Lafferty
Department of Statistics & Data Science
Yale University
Paper Code Documentation 🤗 Model Weights W&B Logs

Abstract

Relational reasoning is a central component of generally intelligent systems, enabling robust and data-efficient inductive generalization. Recent empirical evidence shows that many existing neural architectures, including Transformers, struggle with tasks requiring relational reasoning. In this work, we distinguish between two types of information: sensory information about the properties of individual objects, and relational information about the relationships between objects. While neural attention provides a powerful mechanism for controlling the flow of sensory information between objects, the Transformer lacks an explicit computational mechanism for routing and processing relational information. To address this limitation, we propose an architectural extension of the Transformer framework that we call the Dual Attention Transformer (DAT), featuring two distinct attention mechanisms: sensory attention for directing the flow of sensory information, and a novel relational attention mechanism for directing the flow of relational information. We empirically evaluate DAT on a diverse set of tasks ranging from synthetic relational benchmarks to complex real-world tasks such as language modeling and visual processing. Our results demonstrate that integrating explicit relational computational mechanisms into the Transformer architecture leads to significant performance gains in terms of data efficiency and parameter efficiency.
Sensory and Relational Attention
Figure: Sensory and Relational Attention in the Dual Attention Transformer. Standard self-attention retrieves sensory information $v_i$ about the attributes of individual objects while relational attention retrieves relational information $r(x, y_i)$ about the relationship between the objects in the context and the receiver. Each relation is tagged with a symbol $s_i$ which acts as an abstract variable identifying the sender. In both cases, information is aggregated according to the attention scores $\alpha_i$, which are computed by a softmax over inner products of queries and keys.

Summary of Paper

The Transformer architecture can be understood as an instantiation of a broader computational paradigm implementing a form of neural message-passing that iterates between two operations: 1) information retrieval (self-attention), and 2) local processing (feedforward block). To process a sequence of objects $x_1, \ldots, x_n$, this general neural message-passing paradigm has the form

$$ \begin{align*} x_i &\gets \mathrm{Aggregate}(x_i, {\{m_{j \to i}\}}_{j=1}^n)\\ x_i &\gets \mathrm{Process}(x_i). \end{align*} $$

In the case of Transformers, the self-attention mechanism can be seen as sending messages from object $j$ to object $i$ that are encodings of the sender's features, with the message from sender $j$ to receiver $i$ given by $m_{j \to i} = \phi_v(x_j)$. These messages are then aggregated according to some selection criterion based on the receiver's features, typically given by the softmax attention scores.

We posit that there are essentially two types of information that need to be routed between objects under this general computational paradigm for sequence modeling: 1) sensory information describing the features and attributes of individual objects, and 2) relational information about the relationships between objects. The standard attention mechanism of Transformers naturally encodes the former, but does not explicitly encode the latter.

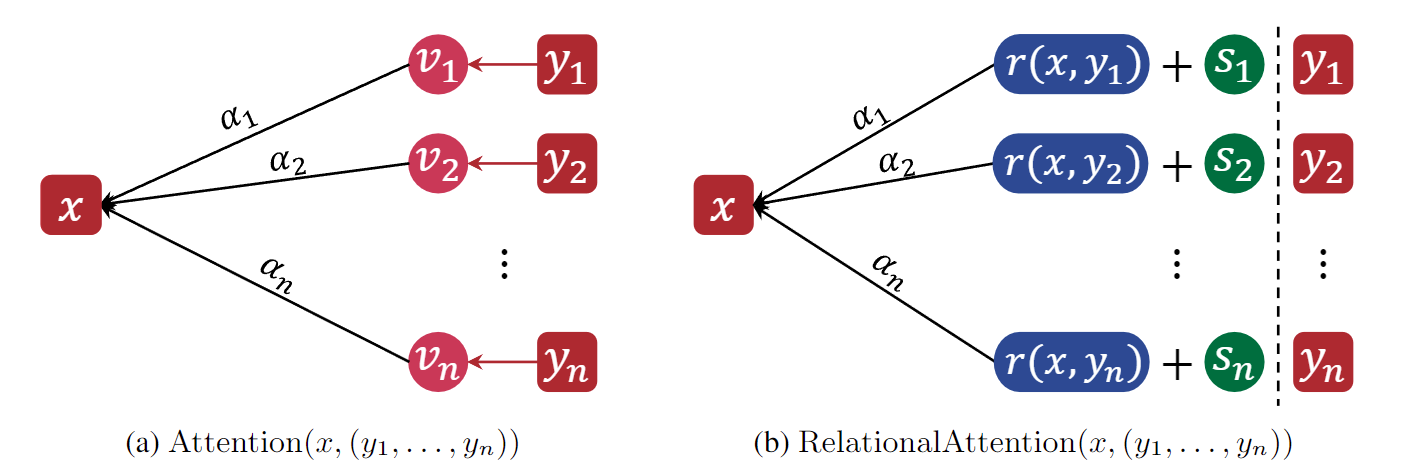
To capture routing relational information between objects, we propose a novel attention mechanism called relational attention. Under the message-passing lens, in relational attention, the message from object $j$ to object $i$ is $m_{j \to i} = (r(x_i, x_j), s_j)$: the relation between the sender and the receiver $r(x_i, x_j)$ tagged with the identity of the sender $s_j$. The relation $r(x_i, x_j)$ is represented by an inner product of feature maps, capturing a comparison of the two objects' features under different filters. The identity of the sender is encoded by a vector $s_j$ that we call object $j$'s "symbol"---it acts as a pointer to the object, enabling a relation-centric representation that is disentangled from sensory information.

$$ \begin{align*} \mathrm{RelationalAttention}(x, (y_1, \ldots, y_n)) &= \sum_{i=1}^{n} \alpha_i(x, \boldsymbol{y}) \left( r(x, y_i) W_r + s_i W_s \right), \\ \alpha(x, \boldsymbol{y}) &= \mathrm{Softmax}\big(\big[\langle \phi_{q, \ell}^{\mathrm{attn}}(x), \phi_{k, \ell}^{\mathrm{attn}}(y_i)\rangle\big]_{i=1}^{n}\big) \in \Delta^n,\\ r(x, y) &= \big(\langle \phi_{q, \ell}^{\mathrm{rel}}(x), \phi_{k, \ell}^{\mathrm{rel}}(y)\rangle\big)_{\ell \in [d_r]} \in \mathbb{R}^{d_r},\\ (s_1, \ldots, s_n) &= \mathrm{SymbolRetriever}(\boldsymbol{y}; S_{\mathrm{lib}}). \end{align*} $$

In relational attention, there exists two sets of query/key feature maps. $\phi_{q, \ell}^{\mathrm{attn}}, \phi_{k, \ell}^{\mathrm{attn}}$ are learned feature maps that control the selection criterion for which object(s) in the context to attend to (i.e., they are used to compute the attention scores $\alpha(x, \boldsymbol{y}) \in \Delta^n$). $\phi_{q, \ell}^{\mathrm{attn}}, \phi_{k, \ell}^{\mathrm{attn}}$ are learned feature maps that represent the relationship between pairs of objects through inner product comparisons $\langle \phi_{q, \ell}^{\mathrm{rel}}(x), \phi_{q, \ell}^{\mathrm{rel}}(y)\rangle$. The $\mathrm{SymbolRetriever}$ learns a library of symbols $S_{\mathrm{lib}}$ and assigns a symbol to each object acting as a pointer or identifier. We consider three symbol assignment mechanisms that identify objects via: their absolute position in the sequence, their position relative to the receiver, or an equivalence class over their features.

To develop a model that supports both fundamental types of information (sensory and relational), we propose dual attention---a variant of multi-head attention composed of two types of attention heads. Standard self-attention heads handle routing sensory information between objects while relational attention heads handle routing relational information between objects. This gives rise to the Dual Attention Transformer, a versatile sequence model with both sensory and relational inductive biases.

An algorithmic description of Dual Attention.

Highlights of Experiments

We empirically evaluate the Dual Attention Transformer (abbreviated, DAT ) architecture on a range of tasks spanning different domains and modalities, with the goal of assessing the impact of relational computational mechanisms in complex real-world tasks.

Relational Reasoning

The first set of experiments evaluates the data-efficiency of DAT on visual relational reasoning tasks. We consider the “Relational Games” benchmark which is used for evaluating relational architectures. The learning curves depicted in the plot below show that DAT is significantly more data-efficient compared to a Transformer in learning relational tasks.

Mathematical Problem-Solving

Mathematical problem-solving is an interesting test for neural models because it requires more than statistical pattern recognition---it requires inferring laws, axioms, and symbol manipulation rules. To probe DAT’s abilities in symbolic reasoning in sequence-to-sequence tasks, we evaluate it on a mathematical problem-solving benchmark. We find that DAT outperforms standard Transformers consistently across model sizes.

Visual Processing

In this section, we explore how the relational computational mechanisms introduced into DAT---namely, relational attention---impact visual processing tasks. We evaluate a ViT-style DAT architecture (ViDAT), and compare it against a standard ViT on the CIFAR image recognition benchmarks. We find that the ViDAT architecture outperforms the standard ViT architecture across both datasets, suggesting that the relational computational mechanisms confer benefits in visual processing.

Dataset Model Parameter Count # Layers $d_{\mathrm{model}}$ $n_h^{sa}$ $n_h^{ra}$ Accuracy
CIFAR-10 ViT 7.1M 8 384 12 0 86.4 ± 0.1%
ViDAT 6.0M 8 384 6 6 89.7 ± 0.1%
CIFAR-100 ViT 7.2M 8 384 12 0 68.8 ± 0.2%
ViDAT 6.1M 8 384 6 6 70.5 ± 0.1%

Language Modeling

Language understanding involves processing and organizing relational information, such as syntactic structures, semantic roles, and contextual dependencies, to extract meaning from words and their connections within sentences. We evaluate the impact of the relational computational mechanisms of DAT in language modeling, training models upto 1.3B parameters in size. We observe improvements in data efficiency and parameter efficiency compared to standard Transformers. By visualizing the internal relational representations of trained DAT language models, we find evidence that they encode human-interpretable semantic relations.

Learn More

  • dual-attention Python Package. The dual-attention package published on the Python Package Index implements the Dual Attention Transformer model and its associated layers and modules. The package also includes utilities for visualizing internal representations of pretrained DAT language models as well as loading pretrained model checkpoints from Huggingface.
  • Documentation. The dual-attention documentation provides a user guide for the different components of the package.
  • Experiment Code. This is the github repository used throughout the development of the project. It includes the code used to run each set of experiments in the paper together with instructions for reproducing our experimental results.
  • Experimental Logs. This online portal provides full experimental logs through the W&B experiment tracking tool. For each experimental run, this includes the git commit ID associated with the version of the code that was used to run the experiment, the script and command line arguments associated with the experimental run, the hardware used for that run, and metrics tracked over the course of training.
  • Huggingface Collection. This is a collection of model checkpoints and apps associated with the Dual Attention Transformer. In particular, language models trained on the Fineweb dataset can be directly loaded from Huggingface through the dual-attention package (see documentation). In addition, we also created apps for exploring trained DAT language models:

BibTeX

@misc{altabaa2024disentanglingintegratingrelationalsensory,
      title={Disentangling and Integrating Relational and Sensory Information in Transformer Architectures},
      author={Awni Altabaa and John Lafferty},
      year={2024},
      eprint={2405.16727},
      archivePrefix={arXiv},
      primaryClass={cs.LG},
      url={https://arxiv.org/abs/2405.16727},
}